| Quantum Mechanics Solution Manual |
|
© Leon van Dommelen |
|
4.5.1.1 Solution commutea-a
Question:
The pointer state
is one of the eigenstates that 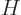 ,
, 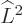 , and
, and 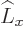 have in common. Check that it is not an eigenstate that
have in common. Check that it is not an eigenstate that 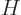 ,
, 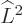 , and
, and 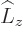 have in common.
have in common.
Answer:
It is an eigenstate of 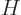 and
and 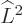 , but not of
, but not of 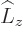 . Since the
. Since the 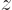 angular momentum of a
angular momentum of a 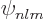 state is
state is 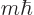 , the combination above has a 50%/50% probability that the
, the combination above has a 50%/50% probability that the 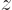 angular momentum is
angular momentum is 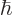 or
or 
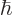 .
.
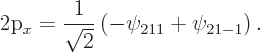
![]()
![]() ,
,![]() .
.![]()
![]()
![]() ,
,![]()
![]()
![]()
![]() .
.