|
|
|
|
|
Next: 5. Multiple-Particle Systems |
|
The hydrogen atom studied earlier is where full theoretical analysis
stops. Larger systems are just too difficult to solve analytically.
Yet, it is often quite possible to understand the solution of such
systems using approximate arguments. As an example, this section
considers the ![]() -
-
The general approach will be to compute the energy of the ion, and to show that the energy is less when the protons are sharing the electron as a molecule than when they are far apart. This must mean that the molecule is stable: energy must be expended to take the protons apart.
The approximate technique to be used to find the state of lowest energy is a basic example of what is called a “variational method.”
First the Hamiltonian is needed. Since the protons are so much heavier than the electron, to good approximation they can be considered fixed points in the energy computation. That is called the “Born-Oppenheimer approximation”. In this approximation, only the Hamiltonian of the electron is needed. It makes things a lot simpler, which is why the Born-Oppenheimer approximation is a common assumption in applications of quantum mechanics.
Compared to the Hamiltonian of the hydrogen atom of section
4.3.1, there are now two terms to the potential energy, the
electron experiencing attraction to both protons:
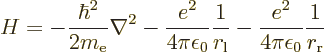 |
(4.74) |
| (4.75) |
The hydrogen ion in the Born-Oppenheimer approximation can be solved
analytically using prolate spheroidal coordinates.
However, approximations will be used here. For one thing, you learn
more about the physics that way.
Key Points
- In the Born-Oppenheimer approximation, the electronic structure is computed assuming that the nuclei are at fixed positions.
- The Hamiltonian in the Born-Oppenheimer approximation has been found. It is above.
The fully dissociated state is when the protons are very far apart and there is no coherent molecule, as in figure 4.14. The best the electron can do under those circumstances is to combine with either proton, say the left one, and form a hydrogen atom in the ground state of lowest energy. In that case the right proton will be alone.
According to the solution for the hydrogen atom, the electron loses 13.6 eV of energy by going in the ground state around the left proton. Of course, it would lose the same energy going into the ground state around the right proton, but for now, assume that it is around the left proton.
The wave function describing this state is just the ground state
![]()
![]()
| (4.76) |
Similarly the wave function that would describe the electron as being
in the ground state around the right proton will be denoted as
![]() ,
,
| (4.77) |
Key Points
- When the protons are far apart, there are two lowest energy states,
and in which the electron is in the ground state around the left, respectively right, proton. In either case there is an hydrogen atom plus a free proton. ,
When the protons get a bit closer to each other, but still well apart,
the distance ![]()
![]()
![]()
![]()
![]()
![]()
However, assuming that the right proton stays sufficiently clear of
the electron wave function, the distance ![]()
![]()
![]()
![]()
![]()
![]()
![]()
Moreover, the decrease in energy due to the electron/right proton attraction is balanced by an increase in energy of the protons by their mutual repulsion, so the total energy of the ion remains the same. In other words, the right proton is to first approximation neither attracted nor repelled by the neutral hydrogen atom on the left. To second approximation the right proton does change the wave function of the electron a bit, resulting in some attraction, but this effect will be ignored.
So far, it has been assumed that the electron is circling the left proton. But the case that the electron is circling the right proton is of course physically equivalent. In particular the energy must be exactly the same by symmetry.
Key Points
- To first approximation, there is no attraction between the free proton and the neutral hydrogen atom, even somewhat closer together.
The approximate energy eigenfunction ![]()
![]()
| (4.78) |
Note that the constants ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
A particularly interesting case is the antisymmetric
one, ![]()
![]()
![]()
![]() .
.
The reason is that ![]()
![]()
This is actually a quite weird result. You combine two states, in
both of which the electron has some probability of being at the
symmetry plane, and in the combination the electron has zero
probability of being there. The probability of finding the electron
at any position, including the symmetry plane, in the first state is
given by ![]() .
.![]() .
.![]() .
.
Instead of adding physically observable probabilities, nature
squares the unobservable wave function
![]()
![]() ,
,
The most important combination of ![]()
![]()
symmetric
one, ![]()
![]()
![]() .
.![]() .
.
A state in which the electron is shared is truly a case of the
electron being in two different places at the same time. For if
instead of sharing the electron, each proton would be given its own
half electron, the expression for the Bohr radius, ![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]() ;
;![]()
Key Points
- This subsection brought home the physical weirdness arising from the mathematics of the unobservable wave function.
- In particular, within the approximations made, there exist states that all have the same ground state energy, but whose physical properties are dramatically different.
- The protons may
share the electron.In such states there is a probability of finding the electron around either proton.
- Even if the protons share the electron equally as far as the probability distribution is concerned, different physical states are still possible. In the symmetric case that the wave functions around the protons have the same sign, there is increased probability of the electron being found in between the protons. In the antisymmetric case of opposite sign, there is decreased probability of the electron being found in between the protons.
The previous two subsections described states of the hydrogen molecular ion in which the electron is around a single proton, as well as states in which it is shared between protons. To the approximations made, all these states have the same energy. Yet, if the expectation energy of the states is more accurately examined, it turns out that increasingly large differences show up when the protons get closer together. The symmetric state has the least energy, the antisymmetric state the highest, and the states where the electron is around a single proton have something in between.
It is not that easy to see physically why the symmetric state has the lowest energy. An argument is often made that in the symmetric case, the electron has increased probability of being in between the protons, where it is most effective in pulling them together. However, actually the potential energy of the symmetric state is higher than for the other states: putting the electron midway in between the two protons means having to pull it away from one of them.
The Feynman lectures on physics, [22], argue instead that in the symmetric case, the electron is somewhat less constrained in position. According to the Heisenberg uncertainty relationship, that allows it to have less variation in momentum, hence less kinetic energy. Indeed the symmetric state does have less kinetic energy, but this is almost totally achieved at the cost of a corresponding increase in potential energy, rather than due to a larger area to move in at the same potential energy. And the kinetic energy is not really directly related to available area in any case. The argument is not incorrect, but in what sense it explains, rather than just summarizes, the answer is debatable.
Key Points
- The energies of the discussed states are not the same when examined more closely.
- The symmetric state has the lowest energy, the antisymmetric one the highest.
The objective of this subsection is to use the rough approximations of the previous subsections to get some very concrete data on the hydrogen molecular ion.
The idea is simple but powerful: since the true ground state is the
state of lowest energy among all wave functions, the best among
approximate wave functions is the one with the lowest energy. In the
previous subsections, approximations to the ground state were
discussed that took the form ![]() ,
,![]()
![]()
Note that all that can be changed in the approximation
![]()
![]()
![]()
![]() ,
,![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
This sort of method is called a “variational method” because at the minimum of energy, the
derivatives of the energy must be zero. That in turn means that the
energy does not vary with infinitesimally small changes in the
parameters ![]()
![]()
![]()
![]() .
.
To find the minimum energy is nothing that an engineering graduate
student could not do, but it does take some effort. You cannot find
the best values of ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 1
1
You do want to evaluate the energy of the approximate states accurately as the expectation value. If you do not find the energy as the expectation value, the results may be less dependable. Fortunately, finding the expectation energy for the given approximate wave functions can be done exactly; the details are in derivation {D.21}.
If you actually go through the steps, your print-out should show that
the minimum energy occurs when ![]()
![]()
![]() ,
,
Key Points
- The best approximation to the ground state using approximate wave functions is the one with the lowest energy.
- Making such an approximation is called a variational method.
- The energy should be evaluated as the expectation value of the Hamiltonian.
- Using combinations of
and as approximate wave functions, the approximate ground state turns out to be the one in which the electron is symmetrically shared between the protons.
- The binding energy is the energy required to take the molecule apart.
- The bond length is the distance between the nuclei.
The solution for the hydrogen molecular ion requires elaborate evaluations of inner product integrals and a computer evaluation of the state of lowest energy. As a much simpler example, you can try out the variational method on the one-dimensional case of a particle stuck inside a pipe, as discussed in chapter 3.5. Take the approximate wave function to be:
The variational solution derived in the previous subsection is only a crude approximation of the true ground state of the hydrogen molecular ion. In particular, the assumption that the molecular wave function can be approximated using the individual atom ground states is only valid when the protons are far apart, and is inaccurate if they are 1.3 Å apart, as the solution says they are.
Yet, for such a poor wave function, the main results are surprisingly good. For one thing, it leaves no doubt that a bound state really exists. The reason is that the true ground state must always have a lower energy than any approximate one. So, the binding energy must be at least the 1.8 eV predicted by the approximation.
In fact, the experimental binding energy is 2.8 eV. The found approximate value is only a third
less, pretty good for such a simplistic assumption for the wave
function. It is really even better than that, since a fair comparison
requires the absolute energies to be compared, rather than just the
binding energy; the approximate solution has ![]() 1
1![]() 1
1
The estimated bond length is not too bad either; experimentally the protons are 1.06 Å apart instead of 1.3 Å. (The analytical solution using spheroidal coordinates mentioned earlier gives 2.79 eV and 1.06 Å, in good agreement with the experimental values. But even that solution is not really exact: the electron does not bind the nuclei together rigidly, but more like a spring force. As a result, the nuclei behave like a harmonic oscillator around their common center of gravity. Even in the ground state, they will retain some uncertainty around the 1.06 Å position of minimal energy, and a corresponding small amount of additional molecular kinetic and potential energy. The improved Born-Oppenheimer approximation of chapter 9.2.3 can be used to compute such effects.)
The qualitative properties of the approximate wave function are correct. For example, it can be seen that the exact ground state wave function must be real and positive {A.8}; the approximate wave function is real and positive too.
It can also be seen that the exact ground state must be symmetric around the symmetry plane midway between the protons, and rotationally symmetric around the line connecting the protons, {A.9}. The approximate wave function has both those properties too.
Incidentally, the fact that the ground state wave function must be real and positive is a much more solid reason that the protons must share the electron symmetrically than the physical arguments given in subsection 4.6.5, even though it is more mathematical.
Key Points
- The obtained approximate ground state is pretty good.
- The protons really share the electron symmetrically in the ground state.